In this time of mobile devices and wireless “motes”, flat business organizations, and ad-hoc project teams, fluid trust models will become increasingly important. Interactions between mobile devices will provide valuable services; secure networks will enable interaction while maintaining logical barriers. Implicit certificates enable users and devices to establish trust relationships for
ad-hoc or peer-to-peer network services.
Because implicit certificates can be issued frequently, certificate revocation is unnecessary; the CA will simply no longer refresh a user’s certificate. This makes security policy more flexible. For example, if a traveling user’s laptop or smart-phone is stolen, the private key may be stolen with it; but if the private key is associated with a short-lived implicit certificate (say, active for four days), the keys are only temporarily compromised.
Another advantage of using implicit certificates is flexibility in delegating authority. If different members of a team have different responsibilities, implicit certificates can be issued to these members corresponding to these different responsibilities. Only a team member that has responsibility for a specific topic can decrypt messages or documents on that topic.
Coupled with its flexibility advantages, the ECQV implicit certificate scheme detailed below provides the functional benefits of ordinary certificates, but with lower processing and storage costs, especially when used in an authenticated key agreement scheme, such as ECMQV, or in a signature scheme such as ECDSA. This makes it ideal in the development of flexible and efficient secure systems.
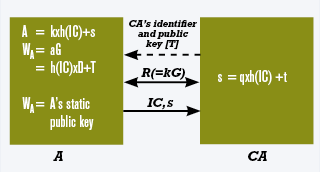
To obtain an implicit certificate:
• A generates a random positive integer k < n and computes a point R on the curve (R = kG). A sends this point R to the certificate authority CA.
• Upon receipt of the point R, the certificate authority CA checks the authenticity of the request received from A.
• CA generates a random positive integer q < n and computes a point Q on the curve (Q = qG). CA then computes the elliptic curve point D, which is the sum of the value R received from A and the value Q generated by CA itself (thus, D = Q + R). CA constructs the to-be-signed certificate data Text, which contains, as a minimum, identifying information according to established procedures of the public key infrastructure and may also contain other information, such as the intended use of the public key, the serial number of the implicit certificate, and the validity period of the implicit certificate.
• CA constructs the implicit certificate IC, which is A’s implicit certificate, which contains the public-key reconstruction data D and the certificate data Text in such a way that this data can be uniquely reconstructed.
• CA signs the implicit certificate IC, by first computing a hash value h(IC) hereof and then calculating the implicit signature s = h(IC) q + t, where t is the CA’s private key.
• CA sends A both the implicit certificate IC and the signature s.
• A uses the implicit certificate IC and signature s to compute its private key:
a = s + k x h(IC) (mod n).
• A may validate whether the implicit certificate IC indeed originated from CA by performing an elliptic curve computation involving the implicit certificate IC and signature s purportedly received from CA, the public-key reconstruction data D derived here from, and the public-key pair (k, R) previously generated by the device itself:
h(IC) R + s G = h(IC) D + T.
This issue of Code & Cipher reviews the first annual Certicom ECC Conference and summarizes some of the key discussions at the event.